Previously we saw how to convert a float to a binary value as well as how to extract the relevant integer and fractional parts from that binary value. We also saw the rules and logic for carrying out addition and subtraction. Now we will look at multiplication and division of these binary values.
Multiplication
There is a quick check that you can do when multiplying before attempting any calculations. If either of the values is 0.0f, the result is always 0.0f. After checking for 0.0f, we extract the integer and fractional parts of each value as before. Multiplying integer parts is a case of shifting the bits left (equivalent to the << operator). Multiplying fractional parts is a case of shifting the bits right (equivalent to the >> operator). For strings that essentially means appending a 0 for integers and pre-pending a 0 for fractions and then a simple addition. As we are calculating the integer and fractional parts separately we need to multiply each fractional part by each integer part and add those results to the total. In order to multiply an integer part by a fractional part we need to ensure that the length of the strings match by padding the integer with 0s at the beginning. That way we don’t adjust the value. For example ![]()
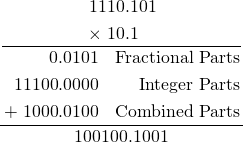
Fractional Parts: ![]() :
:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
// Iterate through the characters from left to right, matching up the first digit on (lhs) of both factors for (const auto rightDigit : right) { if (rightDigit == '1') { const string zeros(scale, '0'); const auto valueToAdd = zeros + left; bool carry = false; result = addBinaryFractions(result, valueToAdd, carry); } ++scale; } |
Integer Parts: ![]() :
:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
// Iterate through the characters from right to left, matching up the last digit on (rhs) of both factors for (auto r = rightLength - 1; r >= 0; --r) { if (right[r] == '1') { const string zeros(scale, '0'); const auto valueToAdd = left + zeros; result = addBinaryIntegers(result, valueToAdd); } ++scale; } |
Combined parts: ![]() :
:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
// Iterate through each fraction digit updating both result strings each time we encounter a 1 for (const auto fractionDigit : fraction) { if (fractionDigit == '1') { const auto scaledInteger = paddedInteger.substr(0, integerLength - fractionDigitPos); integerResult = addBinaryIntegers(integerResult, scaledInteger); bool carry = false; const auto scaledFraction = paddedInteger.substr(integerLength - fractionDigitPos); fractionResult = addBinaryFractions(fractionResult, scaledFraction, carry); if (carry) integerResult = addBinaryIntegers(integerResult, One); } ++fractionDigitPos; } |
Division
Firstly a couple of checks are required. A denominator of 0.0f is not allowed as the result is undefined. Also a numerator of 0.0f results in 0.0f irrespective of the value of the denominator (as long as it isn’t 0.0f). There is a little trick that can be used in some cases for division. If the denominator consists purely of a fractional part, which is also a rational number, it can be converted from decimal format to fractional format (i.e. ![]() ). Then the division becomes a simple case of multiplication:
). Then the division becomes a simple case of multiplication:
![Rendered by QuickLaTeX.com \[ \frac{\text{numerator}} {\text{denominator}} = \frac{\frac{\text{numerator}}{1}} {\frac{1}{\text{integer}}} = \frac{\text{numerator}}{1} \times \frac{\text{integer}}{1} = \text{numerator} \times \text{integer} \]](https://www.eoinoflynn.com/wp-content/ql-cache/quicklatex.com-3b0da5a3691262529e125024eb3527da_l3.png)
However that doesn’t work for irrational floating point values. A better solution involves converting the denominator to a whole integer. Then the numerator should be scaled by the same amount as the denominator. For example ![]()

Once the denominator has been converted to a whole integer the logic then is:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
// Keep iterating until the result reaches the maximum mantissa size while (integerResult.length() + fractionResult.length() < MantissaSize) { auto divides = false; dividend = remainder.substr(0, index); // The denominator can only divide the dividend if the dividend is at least as long as the denominator if (dividend.length() >= denominator.length()) { string trimmedDividend(dividend); trimZeros(trimmedDividend, true); // We are treating the dividend and the denominator as integers so we can ignore the floating parts if (binaryFloatGreaterThan(trimmedDividend, "0", denominator, "0")) divides = true; else divides = (trimmedDividend == denominator); } if (divides) { // After a division update the remainder const auto subtractionResult = subtractBinaryIntegers(dividend, denominator); remainder = subtractionResult + ((index < remainder.length()) ? remainder.substr(index) : string(index + 1 - remainder.length(), '0')); // if the remainder string length is too short then append extra 0s (index is 0 based so add 1) if (index <= decimalPosition) integerResult.append(One); else fractionResult.append(One); } else { remainder.append(Zero); if (index <= decimalPosition) { // Only add 0s once the first 1 has been added if (integerResult.length() > 0) integerResult.append(Zero); } else { fractionResult.append(Zero); } } ++index; } |
Summary
As we can see there is a bit more work involved with multiplication and division of binary floating point numbers compared to addition and subtraction. However the binary operations are more straightforward compared to their decimal counter parts. With multiplication you are either shifting digits left or right. With division you are simply comparing the size of the denominator to a sub-string from the numerator that is at least as long as the denominator. The operation boils down to a few ‘>’ comparisons. Exploring Binary has a great example of a ‘pencil and paper’ version of binary division for further reading.
Source Code
The source code can be found on Bitbucket

